1.1. Модель Курно

МАЛ. 1.1. Рішення фірми № 1 щодо обсягу виробництва. Вибір фірмою № 1 обсягу виробництва, що максимізує прибуток, залежить від того, скільки, на її думку, вироблятиме фірма № 2. Якщо, на думку фірми № 1, фірма № 2 нічого не вироблятиме, то крива попиту на товари фірми № 1 - це крива ринкового попиту. Відповідна крива граничної виручки позначена ГВ1 (0), і вона перетинає криву граничних витрат ГВт на рівні випуску 50 одиниць. Якщо, на думку фірми № 1, фірма № 2 вироблятиме 50 одиниць, то її крива попиту П1(50) зміщується ліворуч на цю величину. Відповідною кривою граничної виручки тепер є ГВ1 (50). Максимізація прибутку тепер передбачає випуск 25 одиниць. П1 (75) і ГВ1 (75) - це криві попиту та граничної виручки для фірми № 1 тоді, коли, на її думку, фірма № 2 вироблятиме 75 одиниць. Тоді фірма № 1 вироблятиме лише 12,5 одиниць.
Суть моделі Курно полягає в тому, що кожна фірма розглядає рівень виробництва свого конкурента як фіксований, а потім вирішує, скільки потрібно виробляти. Щоб побачити, як діє ця модель, розглянемо, як приймає виробниче рішення фірма № 1. Припустимо, на думку адміністрації фірми № 1, фірма № 2 нічого не вироблятиме. Тоді крива попиту на товар фірми № 1 - це крива ринкового попиту. На мал. 1.1 вона показана кривою П(0), що означає криву попиту для фірми № 1 за умови, що фірма № 2 не виробляє продукції взагалі. На мал. 1.1 також показана крива відповідної граничної виручки ГВ1 (0). Ми припустили, що граничні витрати ГВт1 фірми № 1 постійні. Як показано на графіку, обсяг виробництва фірми № 1, який максимізує прибуток, становить 50 одиниць, що відповідає точці перетину кривих ГВ1(0) та ГВт1. Отже, якщо фірма № 2 не виробляє нічого, фірмі № 1 слід виробляти 50 одиниць.
Припустімо, натомість, що, на думку фірми № 1, фірма № 2 вироблятиме 50 одиниць. Тоді крива попиту для фірми № 1 є крива ринкового попиту, зміщена ліворуч до поділки 50. На мал. 1.1 вона позначена П1 (50), а відповідна крива граничної виручки - ГВ1 (50). Обсяг виробництва фірми № 1, який максимізує прибуток, тепер становить 25 одиниць, що відповідає точці, де ГВ1 (50) = ГВт1. А тепер припустімо, що, на думку фірми № 1, фірма № 2 вироблятиме 75 одиниць. Тоді крива попиту для фірми № 1 - це та сама крива ринкового попиту, зміщена вліво до поділки 75. На мал. 1.1 вона позначена П1 (75), а відповідна крива граничної виручки - ГВ1 (75). Тепер обсяг виробництва, що максимізує прибуток фірми № 1, становить 12,5 одиниць, це відповідає точці на графіку, де ГВ1(75)=ГВт1. Нарешті припустимо, що, на думку фірми № 1, фірма № 2 вироблятиме 100 одиниць. Тоді криві попиту і граничної виручки для фірми № 1 (не показані на малюнку) перетинали б криву її граничних витрат на вертикальній осі; якщо, на думку фірми № 1, фірма № 2 вироблятиме 100 або більше одиниць, то їй не слід виробляти нічого.
Підіб'ємо підсумки: якщо, на думку фірми № 1, фірма № 2 не вироблятиме нічого, вона вироблятиме 50 одиниць; якщо фірма № 2 вироблятиме 50, вона вироблятиме 25; якщо ж фірма № 2 вироблятиме 75, вона вироблятиме 12,5; а якщо, на її думку, фірма № 2 вироблятиме 100 одиниць, то вона не вироблятиме нічого. Обсяг виробництва, що максимізує прибуток фірми № 1, є, таким чином, спадною шкалою обсягу, який, на думку фірми № 1, вироблятиме фірма № 2. Ми називаємо цю шкалу кривою реакції фірми № 1 і позначаємо її К1* (К2). Ця крива зображена на мал. 2.2, де кожна з чотирьох наведених комбінацій обсягу виробництва має позначку «*». Аналогічний аналіз ми можемо виконати для фірми № 2 (тобто визначити кількість, максимізуючу прибуток фірми № 2, вважаючи заданими різноманітні припущення щодо обсягу виробництва фірми № 1). Результатом буде крива реакції для фірми № 2, тобто шкала К2*(К1), що співвідносить обсяг її виробництва із обсягом, котрий, на її думку, вироблятиме фірма № 1. Якщо крива граничних витрат фірми № 2 відрізняється від такої ж кривої фірми № 1, крива її реакції буде також відрізнятись за формою від відповідної кривої для фірми № 1. Наприклад, крива реакції фірми № 2 могла б мати вигляд, як зображено на мал. 1.2.
Крива реакції для кожної фірми підказує їй оптимальний обсяг виробництва за заданого обсягу її конкурента. В точці рівноваги кожна фірма планує обсяг відповідно до кривої своєї реакції, так що рівні виробництва в умовах рівноваги перебувають у точці перетину двох кривих реакції. Такий набір рівнів виробництва називаємо рівновагою Курно. За такої рівноваги кожна фірма реально оцінює обсяг, що вироблятиме її конкурент, і відповідно максимізує свій прибуток.
Зауважте, що рівновага Курно є різновидом рівноваги Неша . Слід пам'ятати, що при рівновазі Неша кожна фірма повністю реалізує свій потенціал, приймаючи як заданий обсяг виробництва конкурентів.
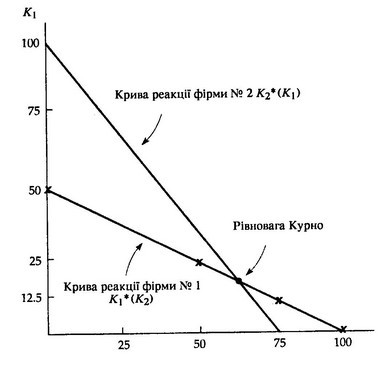
МАЛ. 1.2. Криві реакції фірм і точка рівноваги Курно. Крива реакції для фірми № 1 показує, скільки вона вироблятиме як функцію обсягу того, скільки, на її думку, вироблятиме фірма № 2. Знаки (*) в точках К- 0,50,75 і 100 відповідають прикладам, показаним на мал. 1.1. Крива реакції фірми № 2 показує обсяг її виробництва як функцію обсягу, який, на її думку, вироблятиме фірма № 1. В точці рівноваги Курно кожна з фірм правильно оцінює обсяг виробництва свого конкурента і відтак максимізує власний прибуток. Таким чином, жодна з фірм не порушить цієї рівноваги.
Як результат, жодна з фірм не має причин міняти свою виробничу політику. За рівноваги Курно кожен з дуополістів виробляє ту кількість, яка максимізує його прибуток, приймаючи як заданий обсяг виробництва свого конкурента. Таким чином, жоден з дуополістів не має причин змінювати обсяги виробництва.
Припустімо, що початкові рівні виробництва фірм далекі від рівноваги Курно. Чи будуть фірми вирівнювати обсяги свого виробництва, щоб досягти рівноваги Курно? На жаль, модель Курно нічого не говорить про динаміку перехідних процесів вирівнювання. Справді, протягом будь-якого процесу вирівнювання основне припущення моделі, згідно з яким кожна з фірм припускає, що обсяги виробництва її конкурента фіксовані, не відповідає дійсності. Обсяг виробництва жодної з фірм не буде фіксованим, оскільки обидві фірми вирівнювали б обсяги свого виробництва.
За яких умов для кожної фірми раціональним було б припустити, що обсяг виробництва її конкурента фіксований? Це було б раціональним за тієї умови, якщо обидві фірми встановлюють обсяги свого виробництва лише одноразово, оскільки вони не можуть бути зміненими. Це також було б раціональним за тієї умови, якщо вони перебувають в стані рівноваги Курно, оскільки жодна з фірм не має причин змінювати. обсяг виробництва. Використовуючи модель Курно, ми, отже, маємо зрозуміти специфіку поведінки фірм у стані рівноваги.
Приклад
Розглянемо приклад - дві однакові фірми мають інформацію про лінійну криву ринкового попиту. Це допоможе зрозуміти суть рівноваги Курно і порівняти її з конкурентною рівновагою, а також рівновагою, котра досягається при злитті двох фірм і сприяє об'єднанню зусиль для досягнення певних рівнів виробництва.
Припустимо, наші дуополісти мають таку криву ринкового попиту:
Ц=30-К,
де К - сумарний обсяг виробництва обох фірм (тобто К = К1 + К2). Припустімо також, що обидві фірми мають нульові граничні витрати
ГВт1 = ГВт2 = 0.
Ми можемо визначити криву реакції для фірми № 1 таким чином: для максимізації прибутку фірма встановлює величину граничної виручки на рівні граничних витрат. Сумарна виручка фірми № 1 В1 визначається за рівнянням:
B1=ЦК1 = (30-К)К1
=30К - (К1+К2)К1
=30К1-К21-К2К1
Гранична виручка фірми ГВ1 - це просто додаткова виручка ?В1, що є результатом додаткової зміни обсягу виробництва ?К1:
ГВ1 = ?B1/ ?K1= 30-2K1-2K2
Тепер, прирівнюючи ГВ1 до нуля (граничні витрати фірми) і розв'язуючи рівняння для К1, ми визначаємо:
Крива реакції фірми №1: К1 = 15 - 1/2K2
Ці самі підрахунки справджуються для фірми № 2:
Крива реакції фірми № 2: К2 = 15 - 1/2К1.
Рівні виробництва в стані рівноваги - це значення для К1 і К2, дійсні в точці перетину двох кривих реакцій, тобто величини, отримані при розв'язанні рівнянь. Замінюючи К2 в рівнянні виразом з правої частини рівняння , можна переконатись, що рівні виробництва в стані рівноваги становлять:
Рівновага Курно: К1 = К2 = 10.
Сумарний обсяг виробництва становить К=К1+К2=20, отже, ринкова ціна рівноваги становить Ц = ЗО - К = 10.
На мал. 1.3 показано криві рівноваги Курно та точку рівноваги Курно. Зауважте, що крива фірми № 1 показує її обсяг виробництва в показниках обсягу виробництва фірми № 2. Подібно крива фірми № 2 показує К2 в показниках К1. (Оскільки фірми є ідентичними, обидві криві мають однакову форму. Вони мають різний вигляд, оскільки одна з них задає К1 в показниках К2, а інша виражає К2 в показниках К1). Точка рівноваги Курно перебуває на перетині двох кривих. В цій точці кожна фірма максимізує свій власний прибуток, знаючи обсяг виробництва свого конкурента.
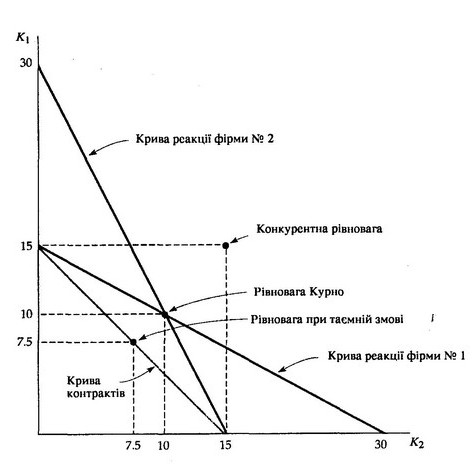
МАЛ. 1.3. Приклад дуополії. Крива попиту задана рівнянням Ц= 30 - К, а граничні витрати обох фірм дорівнюють нулю.У точці рівноваги Курно кожна фірма виробляє 10 одиниць. Контактна крива показує комбінації К1 і К2, які максимізують сумарні прибутки. Якщо фірми змовляться і ділитимуть прибутки порівну, кожна з них вироблятиме 7,5 одиниць. Крім того, показана також конкурентна точка рівноваги, в якій ціна дорівнює граничним витратам, а граничний прибуток дорівнює нулю.
Ми припустили, що між собою конкурують дві фірми. Припустімо, натомість, що антимонопольне законодавство було дещо пом'якшено, і обидві фірми можуть укласти таємний договір. Вони можуть визначити свої обсяги виробництва таким чином, щоб максимізувати сумарний прибуток і ділити цей прибуток порівну. Сумарний прибуток максимізується вибором сумарного обсягу К так, щоб гранична виручка дорівнювала граничним витратам, а ця величина в даному прикладі дорівнює нулю. Сумарна виручка для обох фірм становить
В = ЦК = (ЗО - К)К = 30К - К2,
так що гранична виручка ГВ = ?В/?К=30-2К
Прирівнюючи ГВ до нуля, ми бачимо, що сумарний прибуток максимізується, коли К=15.
Будь-яке комбінування обсягів виробництва К1 і К2, що в сумі дає 15 одиниць, максимізує сумарний прибуток. Крива К1 +К2= 15, яка називається кривою контрактів, визначає, таким чином, усі пари обсягів К1 і К2, які максимізують сумарний прибуток, її показано на мал. 1.3 Якщо фірми домовляться ділити прибутки порівну, то кожна з них вироблятиме половину сумарного обсягу:
К1=К2= 7,5.
Як і слід очікувати, обидві фірми тепер вироблятимуть меншу кількість - і одержуватимуть більші прибутки, ніж у разі рівноваги Курно. На мал. 1.3 показано цю рівновагу, спричинену змовою фірм, та конкурентні рівні виробництва, що визначаються прирівнюванням ціни до граничних витрат. (Ви можете пересвідчитись, що ці рівні становлять К1 = К2 = 15, а це означає, що кожна фірма одержує нульовий граничний прибуток). Зауважте, що результат Курно значно вигідніший для фірм, ніж абсолютна конкуренція, проте не такий виграшний, як здобуток від таємної змови.
Информация, релевантная "1.1. Модель Курно"
- § 2. Зарубежные муниципальные системы.
моделей местного самоуправления. Эти модели отличаются по порядку формирования органов местного самоуправления, предметам ведения местного самоуправления, характеру и особенностям взаимоотношений органов местного самоуправления с органами государственной власти и т.п. Знание и обобщение зарубежного опыта организации местного самоуправления объективно помогает выработать рекомендации по - § 1. Муніципальне право: признаки, предмет и функции
модели организации местной власти, перечень которых не может закрываться. Федеральный закон от 6 октября 2003 г. "Об общих принципах организации местного самоуправления в Российской Федерации" расширил число базовых территориальных, организационных моделей местного самоуправления по сравнению с Федеральным законом от 28 августа 1995 г. "Об общих принципах организации местного самоуправления в - § 1. Правотворческие полномочия в сфере местного самоуправления
модель местного самоуправления. Правотворческие полномочия муниципальных образований распространяются на установление их границ и состава территории, собственной компетенции, форм, порядка и гарантий непосредственного участия населения в решении вопросов местного значения; структуры и порядка формирования органов местного самоуправления, наименования и полномочий выборных, других органов - § 3. Отдельные источники муниципального права
модели местного самоуправления . Данная причина не единственная. Новое конституционное законодательство наделило широкими полномочиями в сфере местного самоуправления субъекты РФ. Отсюда необходимость закрепления в российской Конституции модельной конструкции местного самоуправления, являющейся базовой для субъектов РФ. --- См.: Российское законодательство: - § 1. Муніципальне право как наука и учебная дисциплина
моделях, формулах, других познавательных образованиях и закрепляется на бумажных, электронных, иных материальных носителях. Понятийно-категориальный аппарат - внутренняя форма научного знания. Материальные носители научного знания, такие, как книги, брошюры, рукописи, электронные тексты и т.п., составляют внешнюю форму научного знания и обычно именуются источниками науки. Методология науки - - § 3. Направления современных исследований в отечественной науке муниципального права
моделей местного самоуправления задается законодательством субъектов Федерации. Поэтому в качестве предмета изучения рассматривается организация местного самоуправления отдельных субъектов Федерации. Так, о проблемах организации местного самоуправления в субъектах Федерации размышляет С.А. Авакьян, В.М. Ануфриев. Местное самоуправление в республике Мордовия анализирует А.Р. Еремин. Местное - § 4. Реформы местной власти конца ХХ - начала XXI вв.
моделей местного самоуправления, развитие форм территориального общественного самоуправления. Конкретизация финансовой основы предполагает, во-первых, определение финансовых источников муниципальной самостоятельности в рамках налогового, бюджетного законодательства. Что взять за основу: собственные муниципальные налоги, межбюджетное регулирование или то и другое в определенной пропорции? - § 1. Законодательное определение местного самоуправления
модель местного самоуправления, Закон от 6 октября 2003 г. характеризует его как форму осуществления народом своей власти. Данная форма обеспечивает в пределах, установленных Конституцией РФ, федеральными законами, а в случаях, установленных федеральными законами, - законами субъектов Федерации, самостоятельное и под свою ответственность решение населением непосредственно и (или) через органы - § 2. Местное самоуправление как основа конституционного строя
модель всего общества, государства, национального права в совокупности всех его отраслей. Основы конституционного строя - это и действительное осуществление данных принципов, и то состояние общества, государства, национального права, которое сложилось под их воздействием. Конституционные проявления местного самоуправления. Будучи основой конституционного строя, местное самоуправление выступает - § 1. Территориальная организация местного самоуправления.
модели. Двухуровневая структура территориальной организации местного самоуправления сложилась исторически. В советское время территория деятельности вышестоящих советских органов включала территорию нижестоящих органов. Скажем, территория районного Совета разделялась на территории городских, сельских, поселковых Советов. С переходом в начале 90-х гг. прошлого века от советской системы организации